L'auteur
Simona Ronchi Della Rocca
Dipartimento di Informatica
Università di Torino
ronchi [chez] di.unito.it
Tags
Référence
Simona Ronchi Della Rocca, « Linear Logic and Theoretical Computer Science in Italy : results in Optimal Reduction and Implicit Computational Complexity », Influxus, [En ligne], mis en ligne le 21 novembre 2012. URL : http://www.influxus.eu/article464.html - Consulté le 23 avril 2024.
Linear Logic and Theoretical Computer Science in Italy : results in Optimal Reduction and Implicit Computational Complexity
par
Dedicated to Vito Michele Abrusci in occasion of his 60th birthday
Résumé
Cet article est une courte revue des résultats obtenus par les chercheurs italiens en informatique théorique dans deux domaines spécifiques, les réductions optimales et la complexité implicite, en utilisant des instruments scientifiques issus de la logique linéaire et des logiques dérivées.Abstract
The paper is a brief survey of the work done by the italian scientists in Theoretical Computer Science in two particular research topics, Optimal Reduction and Implicit Computational Complexity, using tools derived from Linear Logics and its variants.Introduction
Linear Logic LL was introduced by Girard in 1986 [Gir87] as a refinement of classical and intuitionistic logic, in particular characterized by the introduction of new connectives (exponentials) which give a logical status to the operations of erasing and copying (corresponding to the structural rules of classical and intuitionistic sequent calculi). In other words, with Linear Logic, logical formulae really become physical resources, with a lot of almost immediate applications to Computer Science, spanning from the representation of operational aspects of programming languages and their evaluation strategies, to a dynamic definition of the notion of computational complexity, from linearity analysis and refined type synthesis for sequential languages, to the semantics of sequential and concurrent programming languages. Since its birth, Linear Logic has taken increasing importance in the field of logic in computer science ; it carried a set of completely original concepts (phase semantics, proof nets, coherent spaces,
geometry of interaction), rediscovered and put to use previous tools (*-autonomous categories, game semantics), and deeply renewed the field. So, Linear Logic is not only an elegant and powerful technical theory but, first of all, a source of methodological guidelines. We learned from the definition of LL that some logical connectives, which were considered atomic, are composite. In fact the essential property of LL is the decomposition of the intuitionistic implication ![]() in
in
![]() . A linear implication
. A linear implication ![]() represents a transformation process, that, taken as input one object belonging to
represents a transformation process, that, taken as input one object belonging to ![]() ,
,
gives as output one object belonging to B. The modality ! denotes a different process, which gives explicit evidence to intensional
properties of the object ![]() to be transformed. These properties describe the potentiality of the object to be either duplicated or deleted during the transformation. So LL supports primitive operators for duplication and erasure, which are only present at a meta-level in the standard approach. Such operators can be used to control how the proofs are built
to be transformed. These properties describe the potentiality of the object to be either duplicated or deleted during the transformation. So LL supports primitive operators for duplication and erasure, which are only present at a meta-level in the standard approach. Such operators can be used to control how the proofs are built
and executed (i.e., normalized). Through the well known connection between logical proofs and functional languages, formalized in the so-called Curry-Howard isomorphism, LL allows to define a computable function as composition of a duplication/erasure operation followed by a linear function. Moreover LL introduced a new approach to proof theory, through the notion of proof-net. Proof-nets are proofs (programs, via Curry-Howard correspondence) characterized by pure geometrical properties (the correctness criteria). They are an essential tool for refining the logical system, for studying its dynamic aspects (proofs normalization) and for characterizing fragments of the system with particular computational properties (like the polarized linear logic or the low complexity systems). Particular notations for proof-nets have been studied, which allow to define normalization procedures based on local operations, making incremental duplications. An interesting application of these properties is the design of interpreters for functional languages using optimal reduction strategies. A mathematical semantics of the cut-elimination in LL has been given through the Geometry of Interaction. LL gave new tools for studying the semantics of computations : coherence spaces, functional domains more refined than the previous Scott domains for studying the denotational semantics, and the game semantics, which is a synthesis of the two classical approaches to semantics, the operational and the denotational one. Game semantics can be fruitfully used for building fully abstract models.
The Light Linear Logic (LLL) [Gir98] is a variant of LL, due to Girard, which further decomposes the duplication operation, so allowing to control the normalization time. It has been a great sort of inspiration for computer scientists, supplying them a technique for modelling programming languages with an explicit resources control, both in space and time.
In Italy LL and its variants has been studied extensively, by a group of researchers from the universities of Torino, Bologna, Roma 3, Roma La Sapienza, Verona and Udine. The investigation about LL started in 1987 inside the EU-project « Typed Lambda Calculus », leaded by Girard, followed by the EU-projet « Linear Logic » leaded by Regnier. Then the research activities of the group continued at a local level, through the PRIN projects « Linear Logic » (leaded by Asperti) and « PROTOCOLLO » (from PROofs TO COmputations through Linear LOgic), « FOLLIA » (FOndazioni Logiche di LInguaggi Astratti di Computazione) and « CONCERTO » (CONtrol and CERTification Of Resources Usage), leaded by myself.
The scientists collaborating to this projects have either mathematical or philosophical or computer science background. This interdisciplinary interaction has been very fruitful, since it allowed to look at the same problems from different points of view. The common interest was a logical approach to computer science, based on the principle of LL.
Here I want to recall just the results in two research lines, the Optimal Reduction and the Implicit Computational Complexity, that are particularly interesting since their possible applications.
I want to point out that this is not a technical paper. The contributions in these two fields have been impressive, both in number and quality, so it would be impossible to give a precise description of them. The bibliography will help the reader interested to some particular technical point.
1. Some basic concepts
Most of the results that will be showed in the next sections will be based on the use of ![]() -calculus, as paradigm of computation. I assume the reader has some acquaintance with it, but I will recall some basic notions about it, just to establish a common vocabulary. More about
-calculus, as paradigm of computation. I assume the reader has some acquaintance with it, but I will recall some basic notions about it, just to establish a common vocabulary. More about ![]() -calculus can be find in [Bar84], whose notations I will use in the following.
-calculus can be find in [Bar84], whose notations I will use in the following.
The set ![]() of terms of
of terms of ![]() -calculus is generated by the following grammar :
-calculus is generated by the following grammar :
![]()
where ![]() ranges over an enumerable set
ranges over an enumerable set ![]() of variables, and
of variables, and ![]() is a binder for variables. A term of the shape
is a binder for variables. A term of the shape ![]() is
is
called abstraction, while a term of the shape ![]() is called application. A context
is called application. A context ![]() is a term with an occurrence of a special constant, the hole, denoted by
is a term with an occurrence of a special constant, the hole, denoted by ![]() , and
, and ![]() denotes the term resulting from filling the hole with a term
denotes the term resulting from filling the hole with a term ![]() ; notice that filling the hole is not a substitution, since free variables of
; notice that filling the hole is not a substitution, since free variables of ![]() can become bound in
can become bound in ![]() .
.
The reduction rule (called ![]() -rule) is the following :
-rule) is the following :
![]()
where ![]() denotes the replacement of every free occurrence of
denotes the replacement of every free occurrence of ![]() by the term
by the term ![]() in
in ![]() , may be preceeded by a renaming of bounded variables for avoiding variables clashes.
, may be preceeded by a renaming of bounded variables for avoiding variables clashes. ![]() is called redex, and it represents the application of the function
is called redex, and it represents the application of the function ![]() to the argument
to the argument ![]() , and
, and ![]() is its reduct, representing in its turn the replacement of the formal parameter
is its reduct, representing in its turn the replacement of the formal parameter ![]() by the actual parameter
by the actual parameter ![]() .
.
The ![]() -reduction is the contextual closure of the
-reduction is the contextual closure of the ![]() -rule, and I will abuse the notation writing
-rule, and I will abuse the notation writing ![]() by denoting that
by denoting that ![]() is obtained from
is obtained from ![]() by reducing a
by reducing a ![]() -redex in it. A term is in normal form if it has no occurrences of redexes, it is normalizing if there is a sequence of
-redex in it. A term is in normal form if it has no occurrences of redexes, it is normalizing if there is a sequence of ![]() -reductions starting from it reaching a normal form, while it is strongly normalizing if every sequence of
-reductions starting from it reaching a normal form, while it is strongly normalizing if every sequence of ![]() -reductions starting from it reaches a normal form. The
-reductions starting from it reaches a normal form. The ![]() -reduction is confluent, so if a term is normalizing then its normal form is unique.
-reduction is confluent, so if a term is normalizing then its normal form is unique.
A term can contain more than one redex, and different choices of the redex to be reduced give rise to different strategies. Formally a strategy is a function from terms to redexes, choosing at every step the redex to be reduced. A strategy is weak if it never chooses a redex under a scope of a ![]() -abstraction ; so a term of the shape
-abstraction ; so a term of the shape ![]() is a weak normal form. Equivalently the weak reduction is the closure of the
is a weak normal form. Equivalently the weak reduction is the closure of the ![]() -rule under applicative contexts, i.e., contexts of the shape
-rule under applicative contexts, i.e., contexts of the shape ![]() or
or ![]() .
.
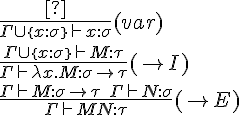
The ![]() -calculus has been used as paradigmatic language for the call-by-name functional computation. In fact, in a redex the argument is passed to the function without being previously evaluated. A call-by-value version of
-calculus has been used as paradigmatic language for the call-by-name functional computation. In fact, in a redex the argument is passed to the function without being previously evaluated. A call-by-value version of ![]() -calculus has been designed by Plotkin [Plo75], starting
-calculus has been designed by Plotkin [Plo75], starting
from the same syntax, but restricting the ![]() -rule, which now becomes a conditional rule :
-rule, which now becomes a conditional rule :
![]()
The set ![]() is called the set of values.
is called the set of values.
The so-called Curry-Howard isomorphism supplies an interesting connection between ![]() -calculus and the Minimal Intuitionistic Logic (MIL) in natural deduction style. Namely formulae of MIL can be assigned as types to terms, in such a way that terms that can be typed share the good properties of the logic, in particular normalization. In fact the isomorphism connects terms to proofs,
-calculus and the Minimal Intuitionistic Logic (MIL) in natural deduction style. Namely formulae of MIL can be assigned as types to terms, in such a way that terms that can be typed share the good properties of the logic, in particular normalization. In fact the isomorphism connects terms to proofs, ![]() -reduction to logical normalization, and normal proofs to terms in normal form. The rules of the type assignment system are shown in Fig.2. The technique has been extended to other logics, certainly in a less natural way. In fact, the three logical rules of MIL naturally correspond to the formation rules of the grammar of the
-reduction to logical normalization, and normal proofs to terms in normal form. The rules of the type assignment system are shown in Fig.2. The technique has been extended to other logics, certainly in a less natural way. In fact, the three logical rules of MIL naturally correspond to the formation rules of the grammar of the ![]() -calculus, while different logics could use constructs that are not immediately connected to the structure of terms, as for example the modality of LL.
-calculus, while different logics could use constructs that are not immediately connected to the structure of terms, as for example the modality of LL.
2. Optimal reduction
The functional languages present, with respect to the imperative ones, the advantage that their properties can be statically checked in an easier way by means of formal techniques. But their use is very limited. One of the reasons is that the available implementations of functional languages are not more efficient than the preexisting imperative ones, being the machine architecture essentially imperative. The problem of finding an optimal implementation of functional languages has been studied by Lévy in his thesis [L78]. He used as paradigmatic functional language the ![]() -calculus, as evaluation step the
-calculus, as evaluation step the ![]() -reduction, and as result of the evaluation of a term its normal form, if it exists. Lévy proved that there is no recursive strategy that is optimal. Fixed a reduction strategy
-reduction, and as result of the evaluation of a term its normal form, if it exists. Lévy proved that there is no recursive strategy that is optimal. Fixed a reduction strategy
there always exists a lambda term for which during the normalization a redex will be duplicated forcing to do at least one beta-step more than the minimal possible amount. Lévy defined an equivalence relation between the different copies of a redex produced during a reduction and proved that, given a redex, it is possible to calculate its equivalence class, i.e. the set of its copies (its family). The strategy reducing in parallel all the redexes of the same family performs a minimal number of beta-steps in the normalization of a lambda term. So the result proved by Lévy is that there is not a sequential optimal strategy, but there is a parallel optimal strategy,
consisting in reducing simultaneously all the redexes belonging to the same family. But Lévy was unable to design an effective algorithm maintaining dynamically the information about the families during the reduction. Much later, in 1990, Lamping [Lam90] designed a reduction algorithm based
on a graph representation of terms, implementing the Lévy’s parallel reduction. Roughly speaking, terms are first transformed into graphs, containing particular nodes, called sharing nodes, taking care of the families management. The graph is reduced using local rewriting rules, and then the result is read back into a term.
LL supplied a theoretical justification of the Lamping’s algorithm. In fact, Gonthier, Abadi and Lévy [GAL92] reformulated Lampings algorithm inside Geometry of Interaction by means of a generalization of Lafonts Interaction Nets [Laf95], so providing a proof of its correctness.
The italian contribution in the field of optimal reduction is twofold, both on the theoretical and the applicative side. Asperti gave a further reformulation of the Lamping’s algorithm and proved its correcteness through a categorical semantics of LL [Asp95]. He also supplied a deep investigation on the complexity of the ![]() -reduction [Asp96]. All the different versions of the algorithm cited before share a common part, the abstract algorithm, whose job is to perform the shared
-reduction [Asp96]. All the different versions of the algorithm cited before share a common part, the abstract algorithm, whose job is to perform the shared ![]() -rule and the duplications of terms, and differ in the bookkeping or oracle part, which takes care of mantaining the information about the families. So a complexity measure needs to consider all these different components. In [AM98] it has been proved that, while the number of parallel
-rule and the duplications of terms, and differ in the bookkeping or oracle part, which takes care of mantaining the information about the families. So a complexity measure needs to consider all these different components. In [AM98] it has been proved that, while the number of parallel ![]() -reduction steps performed by the abstract algorithm is optimal, in the sense of Lévy, the duplication and the bookkeeping job can be exponentially bigger. A further refinement of this result has been given in [Cop02] and [ACM04], where it is proved
-reduction steps performed by the abstract algorithm is optimal, in the sense of Lévy, the duplication and the bookkeeping job can be exponentially bigger. A further refinement of this result has been given in [Cop02] and [ACM04], where it is proved
that yet the mere duplication job is not elementary. Such apparently negative results do not invalidate the notion of Levy’s optimality, but
they say that the number of (parallel) ![]() -steps is not a cost model for the
-steps is not a cost model for the ![]() -calculus. A positive condition for increasing the performance of the Lamping’s algorithm has been given by Coppola and Martini in [CM06] : they proved that, if a term can be typed by Elementary Linear Logic (ELL) formulae, then it can be
-calculus. A positive condition for increasing the performance of the Lamping’s algorithm has been given by Coppola and Martini in [CM06] : they proved that, if a term can be typed by Elementary Linear Logic (ELL) formulae, then it can be ![]() -reduced by the abstract Lamping algorithm, so skipping the bookkeeping job. This check can be effectively performed, since Coppola and myself proved that EAL (the affine version of ELL, sharing the same properties) type inference for
-reduced by the abstract Lamping algorithm, so skipping the bookkeeping job. This check can be effectively performed, since Coppola and myself proved that EAL (the affine version of ELL, sharing the same properties) type inference for ![]() -calculus is decidable [CRDR03,CRDR05]. The proof is constructive, indeed a type inference algorithm is supplied, whose complexity is polynomial in the size of the term. The decidability of the logic EAL was already proved in [DLM04]. Note that the two problems, the decidability of a logic and the decidability of the corresponding type assignment (in the sense of Curry-Howard), are independent and in some sense ortogonal. A recent reflexion on the relation between light logics and optimal reduction can be found in [BCDL07].
-calculus is decidable [CRDR03,CRDR05]. The proof is constructive, indeed a type inference algorithm is supplied, whose complexity is polynomial in the size of the term. The decidability of the logic EAL was already proved in [DLM04]. Note that the two problems, the decidability of a logic and the decidability of the corresponding type assignment (in the sense of Curry-Howard), are independent and in some sense ortogonal. A recent reflexion on the relation between light logics and optimal reduction can be found in [BCDL07].
All these investigations opened a new problem : what is a cost model for the ![]() -calculus ? Dal Lago and Martini make a proposal, using the call-by-value
-calculus ? Dal Lago and Martini make a proposal, using the call-by-value ![]() -calculus equipped with a weak strategy. The proof that this strategy realizes a cost model for the call-by-value
-calculus equipped with a weak strategy. The proof that this strategy realizes a cost model for the call-by-value ![]() -calculus is given in two ways, referring to two different models of computation. In [DLM08] they proved that Turing machines and the call-by-value lambda-calculus can simulate each other within a polynomial time overhead, using the weak evalution strategy. In particular, the cost of a single beta reduction is proportional to the difference between the size of the redex and the size of the reduct. Moreover, in [DLM09] they proved that, always with respect to the same reduction strategy, orthogonal constructor term rewrite systems and the call-by-value
-calculus is given in two ways, referring to two different models of computation. In [DLM08] they proved that Turing machines and the call-by-value lambda-calculus can simulate each other within a polynomial time overhead, using the weak evalution strategy. In particular, the cost of a single beta reduction is proportional to the difference between the size of the redex and the size of the reduct. Moreover, in [DLM09] they proved that, always with respect to the same reduction strategy, orthogonal constructor term rewrite systems and the call-by-value ![]() -calculus can simulate each other with a linear overhead. Orthogonal constructor term rewrite systems and lambda-calculus are thus both polynomially related to Turing machines, taking as notion of cost their natural parameters.
-calculus can simulate each other with a linear overhead. Orthogonal constructor term rewrite systems and lambda-calculus are thus both polynomially related to Turing machines, taking as notion of cost their natural parameters.
On the applicative side, an implementation of Lamping’s algorithm has been given through the reduction machine [BOHM] (Bologna Optimal Higher Order Machine)[AG9898][AGN96], whose implementation is based on the sharing graph technique. This technique is deeply described by Guerrini in [Gue01][Gue05], and it is based on the calculus of sharing graphs, whose properties have been extensively studied in [GMM03,GMM01].
Moreover a parallel implementation of the optimal reduction has been given by Pedicini and others by the PELCR machine (Parallel Enviroment for the Optimal Lambda Calculus Reduction) [CPQ06, PQ00]. PELCR interprets lambda terms, extended with constants a la PCF, in a multiprocessor environment, where communication overhead is reduced by aggregating messages, and the load on processors is dynamically balanced by means
of a fair policy, while the piggyback technique allows to decrease the amount of processors loads information.
3. Implicit Computational Complexity
The widespread diffusion of distributed computer systems has increased the need for program correctness and certification. In particular, guaranteeing and certifying runtime properties is of central importance for computer
networks constituted of small and mobile devices with bounded computational resources that receive programs to be executed from the network itself. In particular time and space complexity are essential aspects for a program, since the termination after a too big amount of time can be as problematic as the non termination, and the lack of space can block the execution. The classical Complexity Theory allows to define and compute the complexity of programs, both in space and in time, but it does not supply techniques for build programs with bounded complexity, or to verify at run time the complexity of their execution. The Implicit Computational Complexity (ICC) aims at studying the computational complexity of programs without referring to a particular machine model, external measuring conditions or particular interpretations, but only by considering
language restrictions or logical/computational principles entailing complexity
properties. So as side effect it offers techniques for building
programming languages with bounded complexity as far as systems suitable for statical verification of program complexity.
The research in Linear Logic met ICC thanks to the observation that
the control of duplications in the proof-nets can be used for limiting the complexity of their reduction. Since only modal formulae can be duplicated, this control can be done by limiting the use of the modality, or by introducing new modalities. The result has been the design of the so called Lights Logics, which are variations of LL where the cut-elimination procedure is bounded in time. The ancestor of these logics is the Bounded Linear Logic (BLL) [GSS92], which is a version of LL in which the cut elimination is polynomial in the size of the proof, and this bound is obtained
by explicitly decorating the !-modality by polynomials. A further refinement is Light Linear Logic (LLL) [Gir98], where the polynomial bound is no more explicit, but it is obtained by means of a stratification realized through a further modality, denoted by ![]() . An ortogonal approach to model polynomiality is the Soft Linear Logic (SLL) by Lafont [Laf04],
. An ortogonal approach to model polynomiality is the Soft Linear Logic (SLL) by Lafont [Laf04],
where the bound is obtained by changing the rule for the introduction of the !-modality, in such a way that the injection ![]() does not hold anymore. All these logics are correct and complete with respect to PTIME, in the sense that every proof can be normalized in polynomial time with respect to its size, and moreover every polytime function can be computed by a proof, according to a suitable coding of numerals and functions. A further characterization is that of the class of elementary functions,
does not hold anymore. All these logics are correct and complete with respect to PTIME, in the sense that every proof can be normalized in polynomial time with respect to its size, and moreover every polytime function can be computed by a proof, according to a suitable coding of numerals and functions. A further characterization is that of the class of elementary functions,
through the Elementary Linear Logic (ELL), introduced by Girard [Gir98] and further studied, in its affine version (EAL) by Danos and Joinet [DJ03]. Here the elementary bound is obtained by making functorial the introduction of the !-modality.
The italian contribution to ICC can be organized according with two lines : a logical line, in which the principles of the Light Logics are investigated, and the metodological one, where these principles are applied to the design of languages with bounded complexity, using a Curry-Howard style approach. I will illustrate now briefly the logical contribution, and after I will speak in a more detailed way about the metodological one, which is more directly related to computer science and applications.
Variations and extensions of light logics have been proposed. Roversi, in [Rov99], gave an extended proof of the completeness of LL. Asperti and Roversi designed an intuitionistic version of LAL (the affine version of LLL), and proved its correctness and completeness with respect to PTIME [AR02]. In [DLH09] Dal Lago and Hofmann proposed a generalization of BLL, where it is possible to quantify over resource variables, so making the logic more expressive while maintaining the
polynomial bound. In [DLRV09], a variant of LL has been introduced which is correct and complete with respect to primitive recursive time, thanks to the introduction of a modal impredicativity. A characterization of the finer complexity classes defined by Blum, Shub and Smale has been made in [BP06]. In [DLB06] Baillot and Dal Lago considered LAL with both fixpoints of formulae and second-order quantifiers and analyze the properties of polytime soundness and polytime completeness for various fragments of this system.
Proof-theoretic studies on the mechanisms allowing to limit the normalization of light logics have been performed. Guerrini, Masini and Martini, in [GMM98] gave an a uniform formal system representing
LL, ELL and LLL, based on an approach using a two dimensional generalization of the notion of sequent, previously introduced by Masini in [Mas92, Mas93] for studying in general the notion of modality, and applied to
LLin [MM93]. A different approach to a uniform presentation of light logics has been given in [Maz06], where a decomposition of the modality of LL has been studied, which allows to characterize LLL, ELL and SLL as subsystems of LL. Further investigations along this line have been made in [BM10,GRV09]. The stratification of LLL has been extended by Roversi and Vercelli in [RV09] : they introduced a multimodal stratified framework called MS, which generates stratified proof-nets whose normalization preserves stratification, and gave a sufficient condition for
determining when a subsystem is strongly polynomial time sound. A purely syntactical criterion for checking the polytime soundness of class of proof-nets properly includind the proof-nets of LAL has been given in [RV10].
Flexibility of the structural proof-theoretic approach to implicit
computational complexity, as described here above, is counterbalanced by
a somewhat surprisingly rigidity. Indeed, despite many efforts, no
satisfactory direct relation exists between light logics and any sub-recursive system designed after other principles, like, for example, recursion theory
[BC92]. Dal Lago, Martini and Roversi [DLMR04] made a step forward in this direction, introducing HOLRR, a purely linear lambda-calculus, extended with constants and a higher-order recursor R, where Leivant’s Ramified recursion [Lei94] embeds directly.
A further problem is to give a semantics justification of the light logics. In fact the different semantics of LL, either operational (based on the Geometry of Interaction) or denotational (based on coherence spaces) do not work anymore for light logics, which need a quantitative semantic interpretation. A general discussion about the notion of quantitative semantics can be found in [DLH05]. The notion of context semantics, which has been first applied to LL and its subsystems by Dal Lago [DL09], has been proved to be a powerful tool. Roughly speaking, the context semantics of a proof-net is a set of paths, describing all its possible computations, that gives a quantitative information on the dynamic of normalization. Namely a notion of weight of the proof-net can be defined in this setting,
which supplies an upperbound on the time needed to normalize it. The context semantics has been used for giving a semantic proof of polytime soundness of LAL [DLH08]. A different approach has been used in [TDFL06], where Tortora De Falco and Laurent used an interactive notion to the semantics of proof-nets, based on the notion of obsessional cliques ;
they applied this technique, introduced in [TdF00, TdF01] to both ELL and SLL. A proof of the elementary bound of ELL based on the Geometry of Interaction is in [BP01]. A semantic account of the execution time, i.e., number of cut-elimination steps, in the untyped proof-nets is given in [DCPTdF].
Let me now illustrate the metodological approach. The basic idea is to use (variants of) the ![]() -calculus as paradigm of functional
-calculus as paradigm of functional
programming languages and types as properties of programs. So extending the Curry-Howard approach to Light Logics, terms can be decorated with formulae inheriting the good properties of the logic we start from, in particular the bound on normalization. But the good properties of proofs are
not easily inherited by ![]() -terms. In particular, there is a mismatch between
-terms. In particular, there is a mismatch between ![]() -reduction in the
-reduction in the ![]() -calculus and cut-elimination in logical systems, which makes it difficult both getting the subject reduction property and inheriting the complexity properties from the logic.
-calculus and cut-elimination in logical systems, which makes it difficult both getting the subject reduction property and inheriting the complexity properties from the logic.
Indeed, some logical rules are not remembered in terms, and constructs that are irreducible in proofs become ![]() -redexes, so loosing
-redexes, so loosing
the complexity bound on the number of ![]() -reductions. Baillot and Terui [TB04] studied the problem in the context of LAL, and designed a type assignment system for
-reductions. Baillot and Terui [TB04] studied the problem in the context of LAL, and designed a type assignment system for ![]() -calculus which characterizes PTIME. Gaboardi and myself designed a system with the same property, but based on SLL [GRDR07, GRDR09]. The result is that, if a term can be typed in one of these two systems, then it is normalizing, and moreover every sequence of
-calculus which characterizes PTIME. Gaboardi and myself designed a system with the same property, but based on SLL [GRDR07, GRDR09]. The result is that, if a term can be typed in one of these two systems, then it is normalizing, and moreover every sequence of ![]() -reductions normalizing it performs a number of steps which is polynomial in the size of the term itself. Moreover both the type systems are FPTIME complete, i.e., every polynomial Turing machine can be encoded by a typable term. So the type assignment system can be used for checking the time complexity of a term. Unfortunately the type inference for such systems is undecidable. But, in [GR09], we proved that the restricted type inference without universal quantification is decidable. Both the systems in [TB04] and [GRDR07] use a proper subsets of the logical formulae, where the modality is not allowed in the right part of the
-reductions normalizing it performs a number of steps which is polynomial in the size of the term itself. Moreover both the type systems are FPTIME complete, i.e., every polynomial Turing machine can be encoded by a typable term. So the type assignment system can be used for checking the time complexity of a term. Unfortunately the type inference for such systems is undecidable. But, in [GR09], we proved that the restricted type inference without universal quantification is decidable. Both the systems in [TB04] and [GRDR07] use a proper subsets of the logical formulae, where the modality is not allowed in the right part of the
implication and under the universal quantifier. This restriction solves the mismatch between ![]() -reduction and the normalization in the logic.
-reduction and the normalization in the logic.
Coppola, Dal Lago and myself studied a different approach in the context of EAL [CDLRDR08, CDLRDR05], characterizing elementary computations.
We used, as paradigmatic language, the call-by-value ![]() -calculus. This choice allows to use as types all the formulae of EAL, since, differently from the
-calculus. This choice allows to use as types all the formulae of EAL, since, differently from the ![]() -reduction, the
-reduction, the ![]() -reduction corresponds exactly to a normalization step in the logic.
-reduction corresponds exactly to a normalization step in the logic.
A logical based characterization of polynomial time in a quantum computational model has been made in [DLMZ09].
The type assignment technique based on SLL has been applied to a characterization of PSPACE in [GMRO8a]. Here the ![]() -calculus has been extended with a conditional operator, and a reduction machine has been defined, in order to measure the space complexity. The result is that if a term can be typed, then it can be reduced to normal form, by this machine,
-calculus has been extended with a conditional operator, and a reduction machine has been defined, in order to measure the space complexity. The result is that if a term can be typed, then it can be reduced to normal form, by this machine,
in a space which is polynomial in its size. Moreover the completeness with respect to the decision problems in PSPACE has been proved, by exploiting the equivalence PSPACE = NPTIME. The non-deterministic polynomial time (NPTIME) has been characterized in [GMR08b].
All these type assignment systems use a natural deduction version of the underlaid logics, but they use different way of building a natural deduction version of the logics, wich have been all originally defined in sequent calculus style. In fact there is no a standard transformation since the presence of the modality, as has been discussed in [RDRR97], in the particular case of the Intuitionistic Linear Logic.
Remember that the ultimate aim of this reserch line, from a computer science point of view, is to supply a criterion on programs, which can be checked statically, and which ensures on the validated programs a time or space complexity bound. All the previous cited systems are complete in an extensional way, i.e., it has been proved that all the functions belonging to the characterized complexity class can be computed by a typed program.
From a programming point of view this kind of completeness is of limited interest. In fact one is interested in designing criteria which are intensionally expressive, that is to say which validate as many
interesting programs as possible. Note that, for example, for a Turing-complete language the class of PTIME programs is non recursively enumerable, and so an intensionally complete criterion would not be decidable. But attempts have been made for designing languages more
expressive and user-friendly than the ![]() -calculus. A typed approach based on LAL has been used in [BGM10], where the language LPL has been designed, by extending the
-calculus. A typed approach based on LAL has been used in [BGM10], where the language LPL has been designed, by extending the ![]() -calculus (and the typing rules) by a recursive construct and pattern matching. LPL is correct and complete with respect to PTIME, and it allows for a more natural programming style.
-calculus (and the typing rules) by a recursive construct and pattern matching. LPL is correct and complete with respect to PTIME, and it allows for a more natural programming style.
In [DLG], Dal Lago and Gaboardi introduced a notion of relative completeness.They define a typed language, whose completeness holds in a relative sense. Indeed, the behaviour of programs can be precisely captured only in presence of a complete oracle for the truth of certain assumptions in typing rules. This is exactly what happens in program logics such as Floyd-Hoares logic, where all the sound partial correctness assertions can be derived provided one is allowed to use all the true sentences of first order arithmetic as axioms. Actually, the typing rules are parameterized on a theory E, so that, while soundness holds independently of the specific E, completeness holds only if E is
sufficiently powerful to encode all total computable functions (i.e. if E is universal). The simpler E, the easier type checking and type inference are ;
the more complex E, the larger the class of captured programs.
Also untyped languages with bounded complexity have been designed, as [Rov96, Rov98], where the language is a variant of ![]() -calculus. While the language is untyped, it is inspired to LAL, in the sense that the control on the complexity of the reduction, that in the logic is made by the modality, is internalized in the reduction rule itself, which can be applied just when the redex has a particular shape. The presence of constants and data structures like lists make the language more expressive than the
-calculus. While the language is untyped, it is inspired to LAL, in the sense that the control on the complexity of the reduction, that in the logic is made by the modality, is internalized in the reduction rule itself, which can be applied just when the redex has a particular shape. The presence of constants and data structures like lists make the language more expressive than the ![]() -calculus itself.
-calculus itself.
Conclusions
The research in Theoretical Computer Science in Italy has been deeply influenced by Linear Logic. In particular in the two areas of Optimal Reduction and Implicit Computational Complexity the logical approach based on LL provided useful tools, and the obtained results could have interesting applications. For example, results in the Optimal Reduction area offer suggestions and tools for an efficient implementation of functional programming languages while those ICC could be applied to the construction of tractable programs and to the verification of quantitative
properties of functional programs. We expect now to widen the application of the theories and typing systems for developing methodological tools for studying quantitative properties of programs in various computational paradigms, e.g., sequential, non-deterministic, probabilistic, quantum.
The applicative spin-off we have in mind is the development of new techniques for software verification in a distribute environment, taking into account quantitative features, e.g., resource usage, time-space complexity, and so on.
Acknowledgements
I would like Vito Michele Abrusci for the work he did in leading the group of Roma 3. He has been the advisor of an impressive amount of PhD students, to which he communicated his enthousiasm for the research and its interdisciplinary vision of the science. He, and all his group, gave an important contribution to all the results collected in this paper.
References
[ACM04] Andrea Asperti, Paolo Coppola, and Simone Martini. (Optimal) duplication is not elementary recursive. Information and Computation, 193:21-56, 2004.
[AG98] Andrea Asperti and Stefano Guerrini. The Optimal Implementation of Functional Programming Languages. Cambridge Tracts in Theoretical Computer Science. Cambridge University Press, 1998.
[AGN96] Andrea Asperti, Cecilia Giovannetti, and Andrea Naletto. The Bologna optimal higher-order machine. Journal of Functional Programming, 6(6):763-810, November 1996.
[AM98] Andrea Asperti and Harry G. Mairson. Parallel beta-reduction is not elementary recursive. In POPL’98, pages 303-315. ACM Press, 1998.
[AR02] Andrea Asperti and Luca Roversi. Intuitionistic light affine logic. ACM Transactions on Computational Logic, 3(1):1-39, January 2002.
[Asp95] Andrea Asperti. Linear logic, comonads and optimal reduction. Fundamenta Informaticae, pages 3-22, 1995.
[Asp96] Andrea Asperti. On the complexity of beta-reduction. In POPL’96, pages 110-118. ACM Press, 1996.
[Bar84] Henk Barendregt. The Lambda-Calculus, its Syntax and Semantics. Stud. Logic Found. Math., vol. 103. North-Holland, 1984.
[BC92] S. Bellantoni and S. Cook. A new recursion-theoretic characterization of the polytime functions. Comp. Complex., 2:97–110, 1992.
[BCDL07] Patrick Baillot, Paolo Coppola, and Ugo Dal Lago. Light logics and optimal reduction : Completeness and complexity. In LICS ’07, pages 421-430. IEEE Computer Society, 2007.
[BGM10] Patrick Baillot, Marco Gaboardi, and Virgil Mogbil. A polytime functional language from light linear logic. In ESOP 2010, volume 6012 of LNCS, pages 104-124, 2010.
[BM10] Patrick Baillot and Damiano Mazza. Linear logic by levels and bounded time complexity. Theoretical Computer Science, 411(2):470-503, 2010.
[BP01] P. Baillot and M. Pedicini. Elementary complexity and geometry of interaction. Fundamenta Informaticae, 45(1-2):1-31, 2001.
[BP06] P. Baillot and M. Pedicini. An embedding of the bss model of computation in light affine lambda-calculus. In LCC’06, 2006.
[CDLRDR05] Paolo Coppola, Ugo Dal Lago, and Simona Ronchi Della Rocca. Elementary affine logic and the call by value lambda calculus. In TLCA’05, volume 3461 of LNCS, pages 131–145. Springer, 2005.
[CDLRDR08] Paolo Coppola, Ugo Dal Lago, and Simona Ronchi Della Rocca. Light logics and the call-by-value lambda calculus. Logical Methods in Computer Science, 4(4), 2008.
[CM06] Paolo Coppola and Simone Martini. Optimizing optimal reduction. a type inference algorithm for elementary affine logic. ACM Transactions in Computational Logic, 7:219-260, 2006.
[Cop02] Paolo Coppola. On the Complexity of Optimal Reduction of Functional Programming Languages. PhD thesis, Università degli Studi di Udine, 2002.
[CPQ06] A. Cosentino, M. Pedicini, and F. Quaglia. Supporting function calls within PELCR. EPTCS, 135(3):107-117, 2006.
[CRDR03] Paolo Coppola and Simona Ronchi Della Rocca. Principal typing for elementary affine logic. In Hofmann M., editor, TLCA 03, volume 2701 of LNCS, pages 90-104. Springer-Verlag, 2003.
[CRDR05] Paolo Coppola and Simona Ronchi Della Rocca. Principal typing for lambda calculus in elementary affine logic. Fundamenta Informaticae, 65(1-2):87-112, 2005.
[DCPTdF] Daniel De Carvalho, Michele Pagani, and Lorenzo Tortora de Falco. A semantic measure of the execution time in linear logic. Theoretical Computer Science. to appear.
[DJ03] Vincent Danos and Jean-Baptiste Joinet. Linear logic and elementary time. Information and Computation, 183(1):123-137, May 2003.
[DL09] Ugo Dal Lago. Context semantics, linear logic and computational complexity. ACM Transactions on Computational Logic, 10(4), 2009.
[DLB06] Ugo Dal Lago and Patrick Baillot. Light affine logic, uniform encodings and polynomial time. Mathematical Structures in Computer Science, 16(4):713-733, 2006.
[DLG] Ugo Dal Lago and Marco Gaboardi. Linear dependent types and relative completeness. In LICS 2011. IEEE Press. to appear.
[DLH05] Ugo Dal Lago and Martin Hofmann. Quantitative models and implicit complexity. In R. Ramanujam and Sandeep Sen, editors, Foundations of Software Technology and Theoretical Computer Science, volume 3821 of LNCS, pages 189-200. Springer, 2005.
[DLH08] Ugo Dal Lago and Martin Hofmann. A semantic proof of polytime soundness of light affine logic. In Third International Computer Science Symposium in Russia, volume 5010 of LNCS, pages 134-145. Springer, 2008.
[DLH09] Ugo Dal Lago and Martin Hofmann. Bounded linear logic, revisited. In Typed Lambda Calculi and Applications, 9th International Conference, Proceedings, volume 5608 of Lecture Notes in Computer Science, pages 80-94. Springer, 2009.
[DLM04] Ugo Dal Lago and Simone Martini. Phase semantics and decidability of elementary affine logic. Theoretical Computer Science, 318(3):409-433, 2004.
[DLM08] Ugo Dal Lago and Simone Martini. The weak lambda-calculus as a reasonable machine. Theoretical Computer Science, 398(1-3):32–50, 2008.
[DLM09] Ugo Dal Lago and Simone Martini. On constructor rewrite systems and the lambda-calculus. In ICALP 09, volume 5556 of LNCS, pages 163–174. Springer, 2009.
[DLMR04] Ugo Dal Lago, Simone Martini, and Luca Roversi. Higher-order linear ramified recurrence. In TYPES’03, volume 3085 of LNCS. Springer, 2004.
[DLMZ09] Ugo Dal Lago, Andrea Masini, and Margherita Zorzi. Quantum implicit computational complexity. Theoretical Computer Science, 2009. to appear.
[DLRV09] Ugo Dal Lago, Luca Roversi, and Luca Vercelli. Taming Modal Impredicativity : Superlazy Reduction. In LFCS09, volume 5407 of LNCS, pages 137-151. Springer Verlag, 2009.
[GAL92] Georges Gonthier, Martin Abadi, and Jean-Jacques Lévy. The geometry of optimal lambda reduction. In POPL 92, pages 15-26. ACM Press, 1992
[Gir87] Jean-Yves Girard. Linear logic. Theoretical Computer Science, 50:1-102, 1987.
[Gir98] Jean-Yves Girard. Light linear logic. Information and Computation, 143(2):175-204, 1998.
[GMM98] Stefano Guerrini, Simone Martini, and Andrea Masini. An analysis of (linear) exponentials based on extended sequents. Logic Journal of the IGPL, 6(5):735-753, 1998.
[GMM01] Stefano Guerrini, Simone Martini, and Andrea Masini. Proof nets, garbage, and computations. Theoretical Computer Science, 253(2):185-237, 2001.
[GMM03] Stefano Guerrini, Simone Martini, and Andrea Masini. Coherence for sharing proof-nets. Theoretical Computer Science, 294(3):379-409, 2003.
[GMR08a] Marco Gaboardi, Jean-Yves Marion, and Simona Ronchi Della Rocca. A logical account of PSPACE. In POPL 2008, pages 121-131. ACM Press, 2008.
[GMR08b] Marco Gaboardi, Jean-Yves Marion, and Simona Ronchi Della Rocca. Soft linear logic and polynomial complexity classes. In LSFA 2007, volume 205 of ENTCS, pages 67-87. Elsevier, 2008.
[GR09] Marco Gaboardi and Simona Ronchi Della Rocca. Type inference for a polynomial lambda-calculus. In TYPES’08, volume 5497 of Lecture Notes in Computer Science, pages 136–152. Springer, 2009.
[GRDR07] Marco Gaboardi and Simona Ronchi Della Rocca. A soft type assignment system for lambda-calculus. In CSL’07, volume 4646 of LNCS, pages 253-267, 2007.
[GRDR09] Marco Gaboardi and Simona Ronchi Della Rocca. From light logics to type assignements : a case study. Logic Journal of the IGPL, Special Issue on LSFA 2007, 17:499-530, 2009.
[GRV09] Marco Gaboardi, Luca Roversi, and Luca Vercelli. A by level analysis of Multiplicative Exponential Linear Logic. In MFCS’09, volume 5734 of LNCS, pages 344-355. Springer, 2009. DOI:10.1007/978-3-642-03816-7, ISBN:978-3-642-03815-0.
[GSS92] Jean Yves Girard, Andr ?e Scedrov, and Phil Scott. Bounded linear logic. Theoretical Computer Science, 97(1):1-66, 1992.
[Gue01] Stefano Guerrini. A general theory of sharing graphs. Theoretical Computer Science, 254:99–151, 2001.
[Gue05] Stefano Guerrini. Sharing implementations of graph rewriting systems. In TERMGRAPH 2004, volume 127 of ENTCS, 2005.
[Lé78] Jean Jacques Lévy. Réductions Correctes et Optimales dans le Lambda Calcul. Thèse de Doctorat d’Etat, University Paris VII, 1978.
[Laf95] Yves Lafont. From proof nets to interaction nets. In Jean-Yves Girard, Yves Lafont, and Laurent Regnier, editors, Advances in Linear Logic, volume 222 of London Mathematical Society Lecture
Note Series, pages 225-247. Cambridge University Press, 1995.
[Laf04] Yves Lafont. Soft linear logic and polynomial time. Theoretical Computer Science, 318(1–2):163–180, 2004.
[Lam90] John Lamping. An algorithm for optimal lambda calculus reduction. In POPL 90, page 1630. ACM Press, 1990.
[Lei94] Daniel Leivant. A foundational delineation of poly-time. Information and Computation, 110(2):391–420, 1994.
[Mas92] Andrea Masini. 2-sequent calculus : A proof theory of modalities. Annals of Pure and Applied Logic, 58(3):229-246, 1992.
[Mas93] Andrea Masini. 2-sequent calculus : Intuitionism and natural deduction. Journal of Logic and Computation, 3(5):533-562, 1993.
[Maz06] Damiano Mazza. Linear logic and polynomial time. Mathematica Structures for Computer Science, 16(6):947-988, 2006.
[MM93] Simone Martini and Andrea Masini. On the fine structure of the exponential rule. In Advances in Linear Logic, pages 197-210. Cambridge University Press, 1993.
[Plo75] Gordon Plotkin. Call-by-name, call-by-value and the ![]() -calculus. Theoretical Computer Science, 1:125–159, 1975.
-calculus. Theoretical Computer Science, 1:125–159, 1975.
[PQ00] M. Pedicini and F. Quaglia. A parallel implementation of optimal lambda-reduction. In ACM Proceedings of PPDP 2000, 2000.
[RDRR97] Simona Ronchi Della Rocca and Luca Roversi. Lambda calculus and intuitionistic linear logic. Studia Logica, 59(3), 1997.
[Rov96] Luca Roversi. A Type-Free Resource-Aware ![]() -Calculus. In CSL’96, volume 1258 of Lecture Notes in Computer Science, pages 399-413. Springer-Verlag, 1996.
-Calculus. In CSL’96, volume 1258 of Lecture Notes in Computer Science, pages 399-413. Springer-Verlag, 1996.
[Rov98] Luca Roversi. A Polymorphic Language which is Typable and Poly-step. In ASIAN’98, volume 1538 of LNCS, pages 43-60. Springer Verlag, 1998.
[Rov99] Luca Roversi. A P-Time Completeness Proof for Light Logics. In CSL’99, volume 1683 of LNCS, pages 469-483. Springer-Verlag, 1999.
[RV09] Luca Roversi and Luca Vercelli. Some Complexity and Expressiveness results on Multimodal and Stratified Proof-nets. In TYPES’08, volume 5497 of LNCS, pages 306-322. Springer, 2009.
[RV10] L. Roversi and L. Vercelli. A structural and local criterion for polynomial time computations. In FOPARA 2009, volume 6324 of LNCS, pages 66-81. Springer, 2010.
[TB04] Kazushige Terui and Patrick Baillot. Light types for polynomial time computation in lambda-calculus. In LICS’04, pages 266-275. IEEE, 2004.
[TdF00] Lorenzo Tortora de Falco. Réseaux, cohérence et expériences obsessionnelles, 2000. PhD thesis, Université Paris 7.
[TdF01] Lorenzo Tortora de Falco. Coherent obsessional experiments for linear logic proof-nets. The Bulletin of Symbolic Logic, 7(1):154-171, 2001.
[TDFL06] L. Tortora De Falco and O. Laurent. Obsessional cliques : a semantic characterization of bounded time complexity. In LICS ’06. IEEE, 2006.
